2415. Номер диска
В известной всем
классической задаче о Ханойских башнях будем считать диски перенумерованными
подряд идущими числами начиная с нуля таким образом, чтобы диску с большим
диаметром соответствовал больший номер.
Наша задача – по
заданному порядковому номеру (нумерация с 1) правильного решения задачи определить порядковый номер диска,
которым осуществляется этот ход.
Считаем, что
исходного количества дисков хватает на затребованное количество ходов.
Вход. Номер интересующего нас хода n (1 ≤ n ≤ 263).
Выход. Вывести
порядковый номер диска, которым осуществляется n-ый ход.
|
Пример
входа |
Пример
выхода |
|
6 |
1 |
РЕШЕНИЕ
ханойские
башни
Анализ алгоритма
Рассмотрим
процесс перекладывания трех дисков.
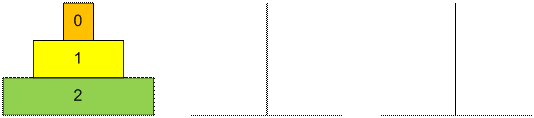
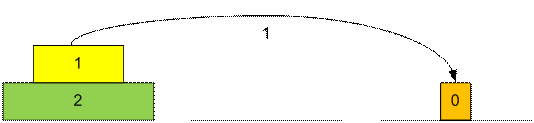

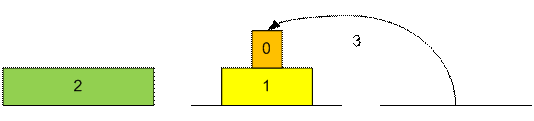
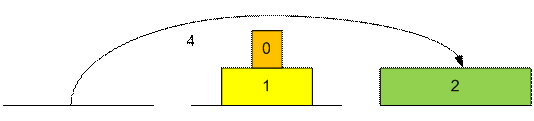

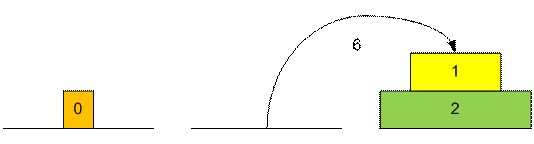
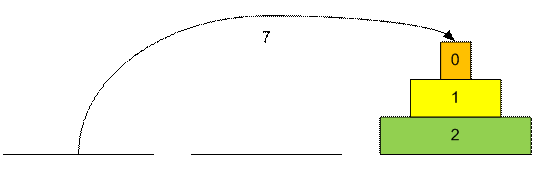
Можно заметить,
что диск номер 0 будет перекладываться во время выполнения ходов 1, 3, 5, 7, 9,
… . Диск номер 1 перекладывается в ходы 2, 6, 10, 14, … (арифметическая
прогрессия с разницей 4). Второй диск перекладывается в ходы 4, 12, 20, …
(арифметическая прогрессия с разницей 8).Следовательно n-ый диск перекладывается в ходы 2n, 2n
+ 2n+1, 2n + 2*2n+1, 2n
+ 3*2n+1, … .
Для определения
номера перекладываемого диска по номеру хода n следует найти двоичном представлении числа n крайний справа номер позиции, в котором находится единица.
Реализация алгоритма
Ищем наименьший
(крайний справа) номер позиции, в которой в двоичном представлении числа n стоит единица. Это и есть номер
перекладываемого диска.
scanf("%lld",&n);
res = 0;
while((n & 1) == 0)
{
n /= 2;
res++;
}
printf("%lld\n",res);
Python реализация
n = int(input())
res = 0
while(n % 2 == 0) :
n //=
2
res += 1
print(res)